In the previous post I tried to summarize the Autobahn paper but its goal, seamlessness, seem convoluted. In this post, I will try to explain it in my own way so that hopefully it can be easier to understand and get myself an internship at Ethereum Foundation 🙂
Background & Motivation
We assume $f$ faulty validators and a total of $n=3f+1$ validators. We will still start by defining blips.
- Blip: a period during which protocol does not make progress. This include network asynchrony, Byzantine leader elected, etc.
Existing practical BFT protocols can be largely categorized as partially synchronous and asynchronous, depending on their network assumptions. Traditional wisdom says that partially synchronous protocols deal poorly with blips. Asynchronous protocols can handle blips well as they proceed at network rate, but perform poorly during good periods due to excessive amount of message exchanges requred to ensure consensus. So this paper asks: why do partially synchronous protocols deal with blips so poorly? Can they do better?
Hangovers
- Hangover: performance degradation caused by blips that lasts after blips end
Since no protocol can make progress during blips, the previous question can be rephrased as, why do partially synchronous protocols experience more serious hangovers than asynchronous protocols and how can we mitigate hangovers.
Take HotStuff as an example, after blips end and timeouts expire, a new benign leader is elected. It will batch client requests into a block, send the block out, collect votes, and send the collected votes with the next block of client requests. Since there are requests coming in during blips, new requests received after blips need to be queued after the old requests, leading to hangovers. So the key to the previous question is, how can we process requests accumulated during blips as fast as possible?
Separate Block Dissemination from Consensus
One existing technique is to separate block dissemination (sending block to other validators) from consensus ordering. The key observation is that consensus messages are often small, whereas blocks themselves are orders of magnitude larger, so removing block dissemination from consensus cirtical path can significantly reduce latency. Aptos, for example, uses Narwhal for block dissemination and Jolteon for consensus.
Autobahn similarly adopts this technique. It has an asynchronous block dissemination layer that ensures blocks can be disseminated even during blips and a consensus layer to pick from these blocks for ordering. However, in a naive implementation, since validators need to possess the blocks proposed by the leader before voting, the leader must pick blocks that all $2f+1$ benign validators have received, or they will request the blocks from peers before voting, moving block dissemination back onto the critical path. Yet a block dissemination layer that guarantees this inevitably require numorous message exchanges. Can we do better?
Proof of Availability (PoA)
Turns out validators do not need to validate the exact requests in blocks during consensus ordering – they can ignore bad requests during execution. So a benign validator can vote if the leader can convince it that the blocks will be available when needed. This weak guarantee only requires one benign validator to persist the block and use collision resistant hashes to ensure Byzantine validators cannot lie about block content. To provide this guarantee, during block dissemination, each validator will broadcast its blocks and wait for $f+1$ votes from peers, which it will combine to form a Proof of Availability (PoA). This process is called Certification of Availability Requests (CAR).
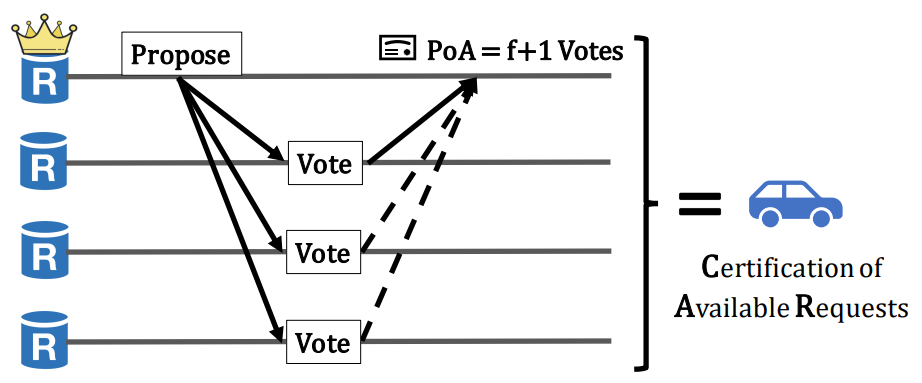
In Autobahn, validators broadcast blocks with the PoA of its parent block, forming a chain. This chain of CARs is called a lane and the last poposed block in a lane is called a tip. Each validator has its own lane. Byzantine validators may not always append new blocks to lane tip, leading to forks. Benign validators will only vote for a block if it has previously voted for its parent and it has not voted for another block by the same proposer at the same height. This way, PoA for one block proves the availability of all its ancestors.
However, since PoA only require $f+1$ votes, there can be blocks with PoAs at the same height and lanes can diverge. The consensus layer will choose one branch to commit.
Consensus
Autobahn can choose any BFT protocol for its consensus. The key is to include as much PoA as possible in the leader’s proposal. Once validators agree on the set of blocks to commit, they can locally decide how these blocks should be ordered locally through some deterministic algorithms.
Validators each manage a local view of all lanes. The leader will pick out the last certified tip (tip with a matching PoA) of every lane in its local view, forming a tip cut. The leader will include this tip cut in its proposal.
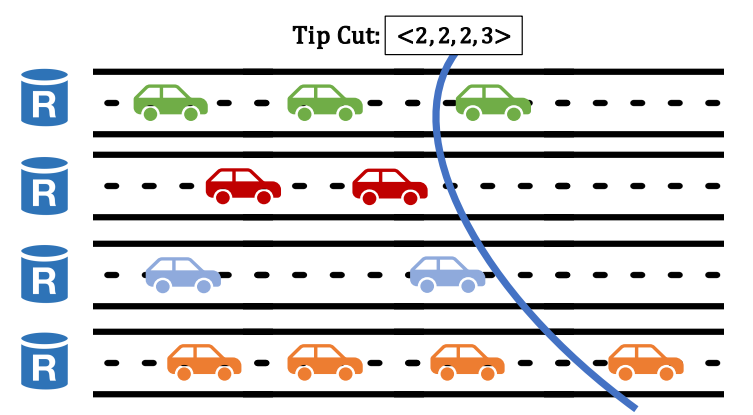
When this proposal is committed, the blocks in the proposed tip cut, along with all its parents up to the last tip cut (committed in the last consensus round), will be committed. This way, after recovering from a blip, a single round of consensus can commit all blocks disseminated during blips, and new requests will not observe any hangovers from here.
A minor problem with this design is that leaders across different views may choose tips from conflicting branches of a lane. In this case, instead of committing all ancestor blocks of the blocks in the current tip cut, Autobahn will only commit up to the block whose parent block is at the same height of the block in the previous tip cut. This means that not all committed blocks are on the same branch of the lane, but ideally this should only happen for Byzantine validators.
The paper uses a linear PBFT-style protocol for consensus, where a round of consensus can be made in 1.5 round trips on the fast path and 2.5 round trips on the slow path. This latency can be reduced by using classic PBFT with all-to-all communication.
